Calculo de volúmenes de solidos en revolución

 

Método de los discos o las arandelas

Al rebanar un sólido de revolución la sección transversal puede ser un disco, si el sólido es macizo o puede ser una especie de arandela (un disco con un agujero en medio), si se trata de un sólido hueco.

Supongamos que se hace girar una región plana alrededor del eje horizontal. De esa región plana tomamos un pequeño rectángulo de anchura Δx, el cual se hace girar en forma perpendicular alrededor del eje axial.

La altura del rectángulo está comprendida entre la curva más externa R(x) y la más interna r(x). Ellas corresponden al radio externo y radio interno respectivamente.

Al hacer esta rotación se genera una arandela de volumen ΔV, dado por:

ΔV = Volumen completo – volumen del agujero (si lo hay)

Recordando que el volumen de un cilindro circular recto es π. radio2 x altura, tenemos:

ΔV = π [R2(x) – r2(x)] Δx

El sólido se puede dividir en multitud de pequeñas porciones de volumen ΔV. Si las sumamos todas, tendremos el volumen completo.

Para ello hacemos tender a 0 el volumen ΔV, con lo cual Δx también se hace muy pequeño, pasando a ser un diferencial dx.Así tenemos una integral:

V = ∫ab π [R2(x) – r2(x)] dx

Figura 3. Método de arandelas. Fuente: Larson. R. Cálculo.

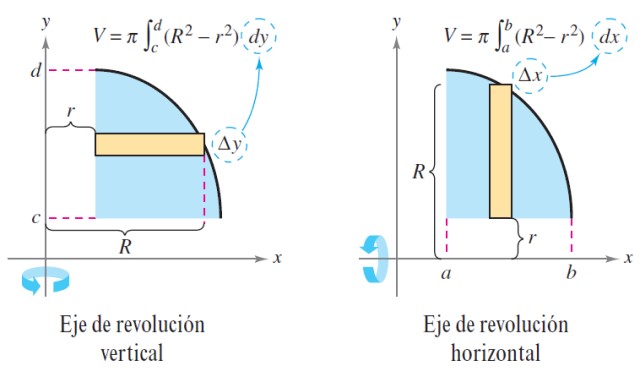
En caso de que el sólido sea macizo, entonces la función r (x) = 0, la rebanada del sólido que se genera es un disco y el volumen queda:

V = ∫ab πR2(x) dx

Cuando el eje de revolución es vertical, las ecuaciones anteriores toman la forma:

V = ∫ab π [R2 (y) – r2 (y)] dy  y V = ∫ab πR2(y) dy

Tipos de sólidos de revolución

Los sólidos de revolución pueden clasificarse según la curva que los genera:

Esfera

Basta con rotar un semicírculo alrededor de un eje que será el diámetro de la esfera de radio R. Su volumen es:

Vesfera = (4/3)πR3

Cono

Para obtener un cono de altura H y radio R,  la superficie que se debe rotar es un triángulo rectángulo, alrededor del eje axial que pasa por uno de los catetos. Su volumen es:

Vcono = (1/3)πHR2

Cilindro

Rotando un rectángulo alrededor de un eje axial que pasa por uno de los lados, que puede ser el lado corto o el lado largo, se obtiene un cilindro circular recto de radio R y altura H, cuyo volumen es:
Vcilindro = πR2H

https://youtu.be/n1U-XC3sygY

https://youtu.be/BgJhiXhuFhk

https://youtu.be/hGeqxBthpMg

Hallar el volumen generado por la rotación de la región plana comprendida entre las curvas:

y = x2;  y=0;  x=2

Alrededor del eje y.

-Lo primero que debemos hacer es graficar la región que va a generar el sólido de revolución y señalar el eje de giro. Lo tenemos en la siguiente gráfica:

Figura 7. Gráfica de las curvas para el ejercicio resuelto. Fuente: F. Zapata con Geogebra.

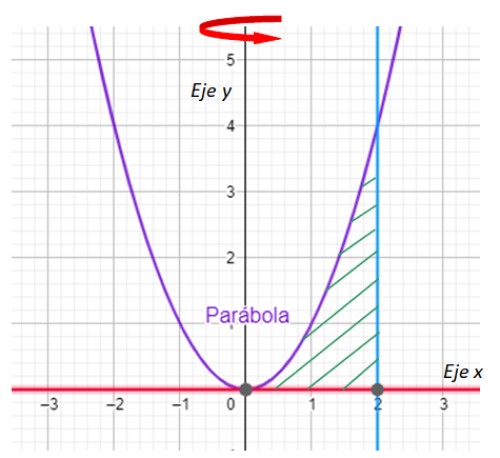
-Ahora se buscan las intersecciones entre la curva y = x2 y la recta x = 2. Por su parte la recta y = 0 no es otro que el eje x.

De la gráfica es fácil advertir que la parábola y la recta se intersectan en el punto (2,4), lo cual se corrobora sustituyendo x = 2 en y = x2.

-Seguidamente se escoge uno de los métodos para calcular el volumen, por ejemplo el método de capas con eje de revolución vertical:

V = ∫ab 2π p(x)h(x)dx

Paso 1: dibujar el rectángulo

Figura 8. Rectángulo para el ejemplo resuelto. Fuente: F. Zapata con Geogebra.

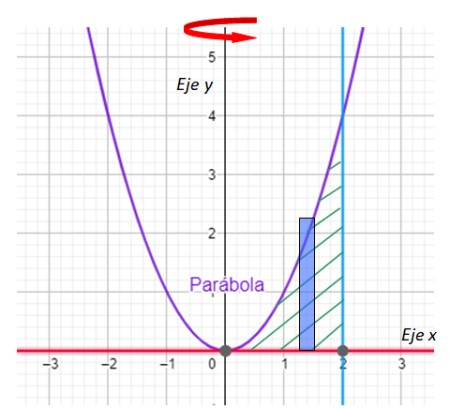
Importante: En el método de capas el lado largo del rectángulo es paralelo al eje de giro.

Paso 2: determinar p(x)

El radio de la capa es x

Paso 3: determinar h(x)

La altura del rectángulo está determinada por la parábola x2.

Paso 4: establecer  y resolver la integral de volumen

La variable de integración es x, la cual varía entre 0 y 2, con esto tenemos los límites de integración. Sustituyendo las expresiones para p(x) y h(x)