INTEGRACION POR PARTES

 Este tema me pareció quizás un poco mas sencillo pero como siempre hay un detalle, para llegar al resultado final es un procedimiento en algunas ocasiones muy largo y quizás por eso puedes llegar a confundirte y olvidar algún paso o saltártelo por error.

Introducción

Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:

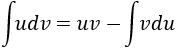
Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).

Aunque se trata de un método simple, hay que aplicarlo correctamente.

Método:

1. El integrando debe ser un producto de dos factores (si no lo es, podemos transformarlo para que lo sea).
2. Uno de los factores será $u$ y el otro será $dv$.
3. Se calcula $du$ derivando $u$ y se calcula $v$ integrando $dv$.
4. Se aplica la fórmula.

• Escoger adecuadamente $u$ y $dv$:

  Una mala elección puede complicar más el integrando.

  Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo $x^3$). Si consideramos $dv=x^3$. Entonces, integrando tendremos que $v=x^4/4$, con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.

  Normalmente, se escogen los monomios (o polinomios) como $u$ para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.

  Algo parecido ocurre con las fracciones (como $1/x$). Si consideramos $dv=1/x$, tendremos $v=\log |x|$ y, probablemente, obtendremos una integral más difícil.

  Como norma general, llamaremos $u$ a las potencias y logaritmos y $dv$ a las exponenciales, fracciones y funciones trigonométricas.

• No cambiar la elección:

  A veces tenemos que aplicar el método más de una vez para calcular una misma integral.

  En estas integrales, al aplicar el método por n-ésima vez, tenemos que llamar $u$ al resultado $du$ del paso anterior y $dv$ al resultado $v$. Si no lo hacemos así, como escoger una opción u otra supone integrar o derivar, estaremos deshaciendo el paso anterior y no avanzaremos.

• Integrales cíclicas:

  En ocasiones, tenemos que despejar la propia integral de la igualdad obtenida para poder calcularla. Por ejemplo, podemos aplicar integración por partes para calcular la integral $\int xdx$, considerando $u=x$ y $dv=dx$. Entonces, obtenemos

  

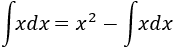
  Observad que tenemos la misma integral en ambos lados, así que podemos operar como si fuese una ecuación (como $x=a-x$, de donde $x=a/2$), despejando en un lado:

  

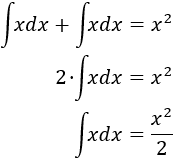
  Otros ejemplos de integrales cíclicas: Integral 10, Integral 17 e Integral 19.

• No hay que olvidar la constante de integración, $C\in R$, al final de cada integral.

EJEMPLO

SOLUCIÓN

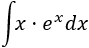
Tenemos el producto $x\cdot e^x$.

Observad que la exponencial no cambia al derivar ni al integrar, así que no importa si le asignamos $u$ ó $dv$.

No ocurre lo mismo con $x$:

• Al derivar se reduce su exponente en 1 y pasa a ser una constante.
• Al integrar aumenta su exponente en 1.

Por tanto, la elección más apropiada es $u=x$ y $du=dx$.

Derivamos $u$ para calcular $du$:

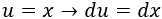
Integramos $dv$ para calcular $v$:

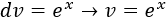
Aplicamos la fórmula de integración por partes:

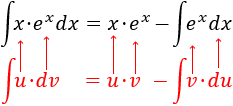
Finalmente, resolvemos la nueva integral (la de la exponencial) y añadimos la constante de integración $C\in R$:

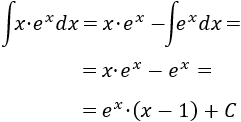
Nota: como ya hemos dicho, es importante escoger $x=u$ para reducir el grado del monomio al derivar. Si por el contrario hubiésemos escogido $x=dv$, entonces $v=\frac{x^2}{2}$, aumentando el grado (de 1 a 2) y complicando más la integral, pues el factor de la exponencial se mantiene igual y nos aparece la integral

$$\int \frac{x^2}{2}\cdot e^{x}dx$$

---

Comentario:

• En la integral anterior hemos considerado $dv=dx$, pero algunos autores habrían escrito simplemente $dv=1$ (es decir, sin $dx$). No es algo que afecte a la resolución de la integral.
• También, podemos encontrar puntos multiplicativos en la fórmula de integración por partes, como en $\int v\cdot du$, que facilitan diferenciar los elementos de la fórmula.

https://youtu.be/6nu-snYlA0Q

https://youtu.be/hvYDrt_Aq2U

https://youtu.be/HHsiy2hyWbI